СоХабр закрыт.

С 13.05.2019 изменения постов больше не отслеживаются, и новые посты не сохраняются.

H Неберущийся интеграл. Берущийся? в черновиках Из песочницы

Математика

Учитель решил проверить знания студента


Обычно на лекциях преподаватели показывают различные примеры, рассказывают какие интегралы берутся, а какие нет. Но в нашем Ленинградском электротехническом университете, видимо, это не так. Преподаватели бывают балуются, а не преподают. На одном из занятий по практике, молодой аспирант сказал: «Вам лектор все объяснил, все рассказал. Я вам все показал, кто не слушал, хм, я не виноват». В одной из задач на дом был довольно интересный интеграл:
image
Я по своей неосведомленности не знал, что данный интеграл не берется и в ответе так и пишется, однако я пытался его решить и решил, но на зачете получил — два!


Некоторые неберущиеся интегралы


Основные интегралы, которые могут спросить на экзамене из ряда неберущихся, были обнаружены Леонардом Эйлером:
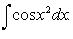image,
image,
image,
image,
image,
image,
image,
image,
image

Решение нтеграла


Дано:
image

а) Для решения интегралов прибегают к методу занесения подынтегральной функции под диффренциал. То есть необходимо найти функцию для замены в интеграле

Известно, что:
image
На основании этого сделаем некоторые преобразования:
image
При этом данное выражение постараемся доказать:
image

б) Введем переменную в интеграле и положим в эту переменную действующую
image

в) Необходимо взять константное число, которое может само себя сократить, для примера возьмем — 2
image

г) Положем двойку знаменателя в переменную, которая является интегрируемой и перейдем к методу занесения под дифференицал
image

д) Завершим начатое
image

е) Так как двойка особо не причем тут, то сделаем иные преобразования
image

На этом все!
математический анализ, Интегралы, Интегралы Эйлера, Неберущиеся интегралы
  maxefect

комментарии (24)

+23
jerom ,  

Честно говоря, какой-то бред написан.

+1
+2 –1
Shybko ,   * (был изменён)

Особенно для тех кто в математике не бум-бум :)
PS: мне тоже не понятно :)

+12
jerom ,  

У меня диплом математика, понять написанное это не помогло.

+4
Suvitruf ,  

Надо спросить того, кто дал инвайт за эту статью)

p.s. @НЛО, я призываю тебя (с)

–5
nadenok ,  

долго втыкал и пытался понять, как это — инвайт за статью ?)

0
rodion_arr ,  

Думаю Вам сюда — habrahabr.ru/info/help/registration/

+7
T-D-K ,  

Что я сейчас прочитал? Как это развидеть?

+8
dginz ,  

«Введем переменную в интеграле и положим в эту переменную действующую» — на этом моменте можно переставать смотреть.

+2
DsideSPb ,   * (был изменён)

Ну, замена переменной. Правда, как-то хитро заявленная и лично мне не очень понятно, зачем.
Мне больше интересен первый переход в пункте (г), который верен только если х = 2. Какое-то слишком суровое колдунство.

PS: здорово, Гинз.

0
bfDeveloper ,  

Замена неправильно проведена. Если заменили x, dx тоже стоило заменить. Иначе дальше придётся учитывать как y = f(x), но тогда все дальнейшие рассуждения не корректны, так как это не учитывается.

0
EvgeshaS ,  

Даже ещё раньше — когда вместо второго замечательного предела написана какая-то ерунда.

+13
nicolnx ,  

> на зачете получил — два!

странно, как же так…

+10
EvgeshaS ,  

Правильность нахождения интеграла можно проверить дифференцированием. По каким переменным автор предлагает дифферецировать выражение n log_y(x) + C, чтобы получить 1/ln(x)?

но на зачете получил — два

Видимо, вполне справедливо. То, что некоторые интегралы не выражаются через элементарные функции — отнюдь не следствие неудачных попыток это сделать, а строгая математематическая теорема.
+8
AdaStreamer ,  

На основании этого сделаем некоторые преобразования:
image
на
image
т.е. вот так вот просто константу а заменили на функцию y ???

+6
kentilini ,  

Ход мыслей рваный, сначала думал, что автор пытается считать вычетами и в комплексной плоскости, потом увидел, что он ввел две переменных(которые по сути одна) и т.д. и т.п. На лицо полное незнание основ мат. аппарата и честно полученная двойка.

На практике используются определенные интегралы, на каком-то диапозоне значений, при чем не все интегралы можно взять точно. Либо производится оценка хвостов, либо интегрируемая функция доопределяется в точках разрывов по некоторым правилам(например разрешением неопределенностей по Тейлору и т.п.)

Автор, учите мат. часть

+4
kbtsiberkin ,  

Действительно, всё, что дальше пункта а), уже ни капельки не годится, а сам пункт а) можно написать в одну строчку, используя правило перехода между основаниями логарифмов.

А место, где вводится константа и вдруг она берёт и оказывается переменной интегрирования — тут и косячок-с, батенька. Ну с чего вдруг? Число оно число и есть, и переменной интегрирования оно стать не может. Чтобы так внести под интеграл x, нужно его же в числителе и писать. Буквенное переобозначение константы не изменит её значения и уж тем более не превратит её в переменную.

Пост сродни тому, как в какой-нибудь комбинированной задачке на смесь термодинамики и электричества сократить газовую постоянную и электрическое сопротивление только лишь потому, что они по недосмотру оказались обозначены R и R.

–9
amarao ,  

Слишком много математики, слишком мало компьютеров.

+2
A1ien ,  

Ошибка присутствует уже во втором преобразовании в числителе: log(x+dx)-log(x)=log((x+dx)/dx) на самом деле: log(x+dx)-log(x)=log((x+dx)/x) дальше все пошло неверно.

0
DsideSPb ,   * (был изменён)

А по-моему, он просто воткнул туда лишнюю дельту. Тоже заметил, но дальше правильно, как будто дельты в знаменателе под логарифмом и не было вовсе. Доказательство как раз в порядке. Ну, сравнительном. Самый абсурд начинается дальше.

0
kbtsiberkin ,  

Да-да, с пунктом (а) всё чисто. Вычислять производные по их определению автор хотя бы научился. Правда, эффект явно недостаточен.

0
+1 –1
kbtsiberkin ,   * (был изменён)

удален. мимо.

+8
paunch ,  
Преподаватели бывают балуются, а не преподают.

С преподавателями тут все в порядке, а вот ваше «баловство» не выдерживает никакой критики. Вы дважды ввели замену, оставляя и старые и новые значения, теперь просто попробуйте все выразить через одну переменную и сделать проверку.
Неразрешимость данного интеграла в элементарных функциях ДОКАЗАНА около 250 лет назад, кстати Эйлером, когда он именно в вашем городе и работал.
+2
Quiz ,  
*робко* Ну вдруг за 250 лет в математике что-то поменялось..?
+5
+6 –1
gvsmirnov ,  

#властискрывают #сумрачныйгений #срывпокровов